Fourier–Mukai transform
The Fourier–Mukai transform or Mukai–Fourier transform is a transformation used in algebraic geometry. It is somewhat analogous to the classical Fourier transform used in analysis.
Definition
Let  be an abelian variety and
be an abelian variety and 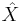 be its dual variety. We denote by
be its dual variety. We denote by 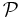 the Poincaré bundle on
the Poincaré bundle on
normalized to be trivial on the fibers at zero. Let  and
and 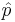 be the canonical projections.
be the canonical projections.
The Fourier-Mukai functor is then
The notation here: D means derived category of coherent sheaves, and R is the higher direct image functor, at the derived category level.
There is a similar functor
Properties
Let g denote the dimension of X.
The Fourier-Mukai transformation is nearly involutive :
It transforms Pontrjagin product in tensor product and conversely.
References
- Mukai, Shigeru (1981). "Duality between
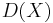 and
and 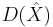 with its application to Picard sheaves". Nagoya Mathematical Journal 81: 153–175. ISSN 0027-7630. http://projecteuclid.org/euclid.nmj/1118786312.
with its application to Picard sheaves". Nagoya Mathematical Journal 81: 153–175. ISSN 0027-7630. http://projecteuclid.org/euclid.nmj/1118786312.
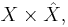
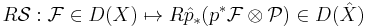
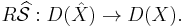
![R\mathcal S \circ R\widehat{\mathcal S} = (-1)^\ast [-g]](/2012-wikipedia_en_all_nopic_01_2012/I/ac6303137b90dc29b18ff292c0709722.png)
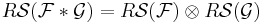
![R\mathcal S(\mathcal F \otimes \mathcal G) = R\mathcal S(\mathcal F) \ast R\mathcal S(\mathcal G)[g]](/2012-wikipedia_en_all_nopic_01_2012/I/ae282b672bca8a904e2ab319a95eddea.png)